Transmission Lines (Part II): More on Bandwidth vs. Rise Time

Figure 1: In the frequency domain (right), a near-ideal
square wave displays predictable 1/f amplitude dropoff

We began this series about transmission lines by thinking about some pertinent principles and relationships that can help form our thinking about the topic. In particular, we'd covered the relationship between bandwidth and rise time and why we have this rule of thumb that says that bandwidth can be estimated using 0.35/10-90% rise time.

Another way to look at and/or think of this relationship is in terms of some periodic waveforms, all of which have the same repeat frequency, and the spectra comprising them. At left in Figure 1 is a near-ideal square wave in the time domain, while at right is the same square wave in the frequency domain. As we might expect, the drop offs in amplitude occur in a fashion mirroring what we would predict by hand, almost literally following A = 2/πn.

Figure 2: A longer rise time means decreased bandwidth

If we take that same waveform but increase the rise time, we will have also decreased the bandwidth. And as Figure 2 shows, the first harmonic is of about the same amplitude as in Figure 1 but subsequent harmonics fall off at a much faster rate. So we can clearly see that with a longer rise time, we get less bandwidth because there are fewer high-frequency components of significance in the waveform.

Figure 3: With a distorted waveform, all bets are off

What happens if we take the initial waveform and add some distortion in the form of ringing (Figure 3)? All bets are off, because it's no longer an ideal, or even close to ideal, square wave. The spectrum shows high-frequency peaking at the 7th harmonic and beyond, with many harmonics having amplitudes greater than that of the ideal square wave. Thus, with a distorted waveform, the A = 2/πn rule of thumb no longer applies.

What if we want to determine the bandwidth of a signal for which we don't know the rise time, but we do know the clock frequency? Figure 4 depicts three different clock signals, all with the same frequency but with different rise times. What can we surmise about the bandwidths of these signals?

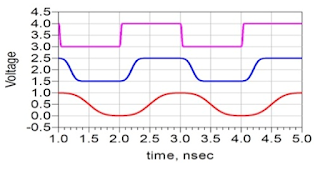Figure 4: Same frequencies, different rise times,
but what are the bandwidths?

We'd stated that bandwidth depends on rise time to the tune of BW = 0.35/10-90% RT. Clearly, the top trace in Figure 4 has the shortest rise time and highest bandwidth. With only the clock frequency, we can arrive at an OK answer for bandwidth, just not a highly accurate one. But sometimes, an OK answer now is better than a better answer later.

To arrive at a bandwidth estimation from a clock frequency, we have to make an assumption about the rise time as a percentage of the waveform's period. If we use, say, 7% as our rise-time assumption, we can use a little algebra as follows:

Thus, we arrive at the oft-cited rule of thumb that says bandwidth equals 5X the clock frequency.

We can think about bandwidth as a property of a signal, but when it comes to an oscilloscope, we are talking about the bandwidth of the instrument. Bandwidth is a critical figure of merit for oscilloscopes.

Figure 5: This graph compares the
frequency response of an RC filter
with that of an oscilloscope

Let's look at a frequency-response comparison of a single-pole RC filter vs. that of an oscilloscope. In Figure 5, the blue curve is that of the single-pole filter, while the red curve is a modern oscilloscope, which we could call a multi-pole filter. Defining "bandwidth" is, at the end of the day, a bit of an arbitrary exercise. The usual definition is the "-3 dB point," or the frequency at which we have about 70% of the signal's amplitude left. If we use that -3 dB point definition, we can verify it for the single-pole filter by literally looking at the time-domain response and measuring the 10-90% rise time.

Sure enough, we find that the 10-90% rise time = 0.35/BW_{3 dB}. Thus, using the term "bandwidth" to mean the -3 dB point for the single-pole filter, the relationship holds.

For the oscilloscope, the transfer function is a little different from that of the single-pole filter. The oscilloscope's red curve in Figure 5 rides higher than that of the single-pole filter, until it falls off a cliff. If we still use the -3 dB point as our definition of bandwidth for the oscilloscope, the relationship of rise time to bandwidth is a little different for a multi-pole response; it's 10-90% RT = 0.45/BW_{3 dB}. But still, if we know the bandwidth of the oscilloscope, then we can determine the shortest rise time we'll be able to observe with it. If, for example, your oscilloscope is rated for a 1-GHz bandwidth, that shortest rise time will be about 450 ps. 

Armed with the background information from this post and the preceding one, next time we can begin applying it to transmission lines.

Previous posts in this series:

Transmission Lines (Part I): Introduction