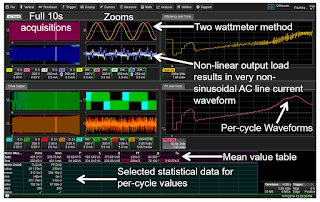
 |
| Figure 1: Screen capture of a 10-s acquisition of AC input and PWM output of a 480-V motor drive |
You need to test, we're here to help.
You need to test, we're here to help.
15 March 2018
An Example of Three-Phase Power Measurements
14 March 2018
Three-Phase Power Calculations
 |
| Figure 1: Three-phase power calculations entail summing of the individual phases's power calculations |
13 March 2018
Power Calculations for Distorted Waveforms
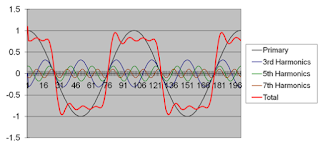 |
| Figure 1: The sum of many sine waves, of varying amplitudes and frequencies, comprises the rough- looking square wave shown in red |
09 March 2018
Power Calculations for Pure Sine Waves
 |
| Figure 1: For a purely resistive load, power = voltage * current, with both vectors in phase |
Back to Basics: AC Sinusoidal Line Current
 |
| Figure 1: A single-phase AC current vector rotates at 50 or 60 Hz |
02 March 2018
More Basics of Three-Phase AC Sinusoidal Voltages
 |
| Figure 1: In the Wye three-phase connection, neutral is present but sometimes inaccessible |
01 March 2018
Transmission Lines (Part V): Reverse-Engineering the DUT
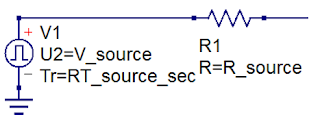 |
| Figure 1: Every DUT can be thought of as a Thevenin voltage source with some internal resistance |
Subscribe to:
Posts (Atom)