Transmission Lines (Part IV): More Essential Principles

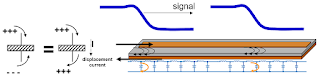
Figure 1: The return current in a transmission line
is as important as the signal current

In our continuing survey of the topic of transmission lines, we'd begun in our last post to cover some essential principles that govern their behavior. We're not quite done with those, so in this post we'll discuss more principles that should be part of the foundation of how you think about interconnects.

To quickly review, the first three principles we covered were:

• All interconnects are transmission lines
• Signals are dynamic
• Signals see an instantaneous impedance

Now we'll add the fourth: The return current is just as important as the signal current. 

For the sake of discussion, let's assume the transmission line depicted in Figure 1 has a characteristic impedance of 50 Ω, and we're about to launch a 1-V signal that will propagate through the line. Now, that 1-V signal will see an instantaneous impedance of 50 Ω, so the current going into that transmission line is 1 V into 50 Ω, or 20 mA.

The current into the signal line is 20 mA, When does it exit the return path at the front end? The answer is "instantaneously." But how can it travel from the signal line to the return path at the beginning of the line when there is an insulating dielectric between them? It turns out that the charging happens just as it does when we get current through a capacitor.

Are there actually little charges flowing through the little "capacitors" shown in Figure 1? No, because there's still the insulating dielectric between the two lines. This was James Clerk Maxwell's big innovation in electromagnetics. We're used to thinking about current in the sense of conduction, but Maxwell posited that there's another equally valid form of current that he termed "displacement current," which is a dE/dT affair as indicated by the plus and minus charges pushing each other around in Figure 1. Whenever the electric field changes, it behaves as though it's a current.

So when we apply 1 V between the signal and return lines in our transmission line, we change the electric field to create displacement current. Wherever the edge is as the signal propagates through the line, we would see our 20 mA of return current. As the signal propagates, we have an associated current loop with two directions: a direction of propagation, which travels from the input end of the transmission line to the output end, and a direction of circulation, which, in this case, is clockwise. These directions are independent of each other. 

Figure 2: Signals reflect when the instantaneous impedance
changes

Now we come to the fifth, and most important, principle of transmission lines: Signals reflect back toward their source if the instantaneous impedance changes. Figure 2 depicts a transmission line in which the instantaneous impedance changes from 50 Ω to 75 Ω. We launch our 1-V signal and it travels along the line until it suddenly sees the impedance change, and we end up with a reflected signal.

How much of the signal gets reflected? That depends on the impedance change, as shown in the formula in Figure 2. If we plug the numbers into that formula, we get a 20% reflection, or 0.2 V. So if we were to measure the voltage on the transmission line, we would see 1.2 V, because we now have two signals traveling on it with different directions of propagation.

An important point to note here is to remember our Principle #2 shown above, which is that signals are dynamic. If we don't have a conception of what's happening here with the impedance change and reflection, and we were trying to figure out signal integrity in this example armed with nothing but the oscilloscope, we would measure only the scalar voltage that appears between the signal and return paths, and that would be 1.2 V as opposed to the 1-V signal we initially launched. So it is critical not to confuse the signal that propagates in a transmission line with the measured voltage at a node. They're not the same thing.

In the next post, we'll run through some more examples, but we'll begin taking account of the impedance of the voltage source.

Previous posts in this series:

Transmission Lines (Part I): Introduction
Transmission Lines (Part II): More on Bandwidth vs. Rise Time
Transmission Lines (Part III): Essential Principles