 |
| Figure 1: An oscilloscope such as Teledyne LeCroy's HDO6054-MS serves a very broad range of applications |
The first step in the selection process is to list all the applications you can think of that you'd use a new oscilloscope for (Figure 1). Of course, it's almost impossible to anticipate everything you might throw at an oscilloscope but it behooves one to try. Once the applications have been determined, as well as the signal characteristics you'd want to measure, then the process becomes more straightforward.
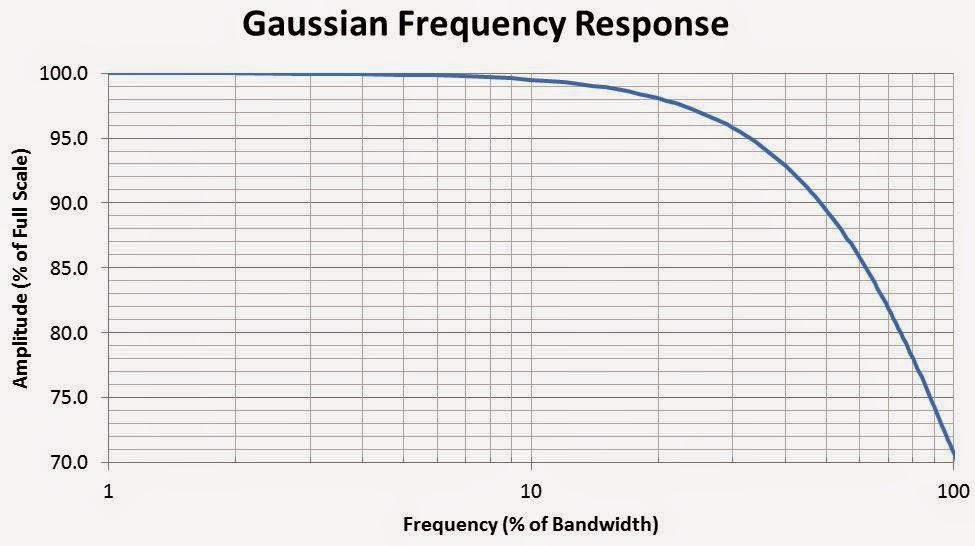 |
| Figure 2: A plot of the Gaussian frequency response of a typical oscilloscope with bandwidth < 2 GHz |
To achieve maximum amplitude accuracy, you want an oscilloscope with a maximum bandwidth of five times the highest frequency component to be measured. Figure 2 tells us that having the highest frequency expected at 20% of the bandwidth yields a 2% amplitude uncertainty.
An oscilloscope's response in the time domain is a function of its step response. The key parameter used to evaluate step response is rise time. The rise time of the step response is related to the oscilloscope's bandwidth by the equation:
Rise time - k/bandwidth
where rise time is in seconds, bandwidth is in Hertz, and k = 0.35 to 0.45 depending on the oscilloscope's frequency response. For bandwidths under 2 GHz, k = 0.35.
The step response of an oscilloscope comes into play when measuring digital signals with fast edges. The rule of thumb for determining bandwidth for digital signals is that the oscilloscope's bandwidth should be 2.5 times the digital signal's bit rate. For example, when measuring serial data with a bit rate of 1 Gb/s, the oscilloscope's bandwidth should be 2.5 GHz. Because the highest data rate for a digital signal is one-half the bit rate, selecting an oscilloscope with a bandwidth of 2.5 times the bit rate means that the fifth harmonic of the data signal will be within the oscilloscope's bandwidth.
In terms of sampling rate, sampling theory fixes the minimum sampling rate for a digital sampling oscilloscope at twice the instrument's bandwidth. In practice, it's usually better to sample at more than 2.5 times the instrument's bandwidth, because higher sampling rates yield higher time resolution. However, doing so comes at the expense of requiring more acquisition memory, so a tradeoff is involved. Oscilloscope accuracy generally improves with oversampling up to five times the bandwidth. Oversampling at more than a factor of five brings diminishing returns.
Acquisition memory length, which is the number of samples in an acquired waveform, is a no-brainer: The longer the memory length in the oscilloscope, the greater will be the duration of the acquired signal:
Captured time interval = memory length/sampling rate
The memory length required reflects the longest signal duration you'll need at a specific sampling rate. To acquire a 200-MHz signal with a duration of 2 ms at a sampling rate of 500 MS/s calls for 1 Mpoints of memory.
A very important—perhaps critical—consideration is vertical resolution, which describes the amplitude precision of the oscilloscope's ADC. Theoretically, an oscilloscope with an 8-bit ADC can resolve the amplitude of a signal to one part in 256. Thus, for a full-scale range of 800 mV, the oscilloscope can resolve the amplitude into a 3.1-mV step at best. Oscilloscopes with 12-bit ADCs can resolve the same signal into steps of 195 μV or 16 times more resolution than the 8-bit oscilloscope.
Why is vertical resolution so important? It comes into play most critically when observing small-signal elements in the presence of larger signals. For example, say you're looking at the "on" voltage for a switching power device, which might be less than 1 V in the presence of the "off"-state voltage, which might be 500 V. An 8-bit oscilloscope would have a theoretical resolution of only 1.9 V/step, while a 12-bit instrument could resolve down to a 0.12-V step.
When shopping for a new oscilloscope, be sure to look over triggering options. Triggering is used to synchronize the acquisition to the waveform being acquired, resulting in a stable waveform display. Simple repetitive waveforms require only a basic edge trigger, but more complex signals with burst-like characteristics call for triggers that can determine specific timing parameters of the waveform, including items such as width, period, or slope. For Teledyne LeCroy, triggers that are sensitive to waveform characteristics are termed SmartTriggers. Teledyne LeCroy also offers qualified and multi-stage triggers that sense relationships between multiple waveforms.
The way in which users interact with an oscilloscope is through its user interface; modern oscilloscopes have a variety of interactive features for control of the instrument. Classic knobs and buttons still appear on the front panels of most oscilloscopes, but these days, oscilloscope operating systems support a range of pointing devices that permit control of the oscilloscope in a fashion not unlike a laptop or desktop computer. For the maximum in interactivity, choose an oscilloscope with a touch screen interface. If you like the knobs and buttons, they'll still be there.
Many users of oscilloscopes want to control their instruments with an external computer, as in an automated test system. This requires the oscilloscope to include remote-control capabilities. Thus, connectivity is a key factor to consider if you're inclined to use an oscilloscope in this fashion. Look for hardware interfaces for protocols such as LAN, LXI, USB, or GPIB, as well as an efficient remote-control command set. Utility software and drivers should be available to help connect the oscilloscope to the user's programming environment.
That's a quick rundown of some of the key criteria you might consider in choosing your next bench oscilloscope. Let us know what's most important to you in your oscilloscopes.
1 comment:
While the graph is close, when I did the calculations the numbers were off around 2%. F(x)=exp^-(f^2/const). For example the graph says .895 at 50% BW but I get .917
Cheers
DrBill
Post a Comment