 |
| Figure 1: Three-phase power calculations entail summing of the individual phases's power calculations |
Figure 1 provides a visual representation of how this works. The formulas for real, apparent, and reactive power are:
- Real power (P): Ptotal = PA + PB + PC
- Apparent power (S): Stotal = SA + SB + SC
- Reactive power (Q): Qtotal = QA + QB + QC
 |
| Figure 2: Line-to-line voltage measurements as shown above must be corrected for magnitude and phase |
Three-Phase Line-to-Line Voltage Measurements
Let's look more closely at the line-to-line exception. As mentioned above, in such cases, the voltage and current will be out of phase, so you need to correct for that by doing a magnitude and phase conversion to a line-to-neutral basis. Referring to Figure 2, the mathematical relationships between VA-B and VA-N are: |
| Figure 3: Voltage is often measured line-to-line but current is measured line-to-neutral |
- Magnitude: VA-B = VA-N * √3
- Phase: VA-B = VA-N - 30°
These relationships hold true for all three phases in a three-phase system. Perhaps you have a system that has voltages and currents in reference to each other (Figure 3). Voltage is often measured from line to line, but often the neutral point is inaccessible, or you may simply prefer line-to-line probing. Meanwhile, current is measured on a line-to-neutral basis. So line-to-line voltages must again be transformed to a line-to-neutral basis. We make the calculations as shown above and sum the phases to find totals in each case.
This method works because we can make mathematical assumptions. If we know two of the three voltages and currents, we can solve for the third. According to Thevenin's Theorem, we can take a line-to-line voltage and a line current, and a line current and a line-to-line voltage, and calculate the three-phase power directly from that information. The mathematical assumptions are as follows:
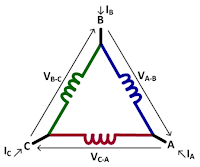 |
| Figure 4: With Delta windings, power balance across all three phases may be elusive in calculations |
The Delta-Winding Exception
In situations involving a Delta winding, voltage is still measured line-to-line: It has to be as the neutral point is inaccessible. The current to be measured is the terminal current, which is not the same thing as the "coil" currents. The calculations as shown above will still be correct, but you may not have power balance across all three phases because you're not really measuring the "coil" current. Still, total three-phase power is still calculated as described above by summing the phases.Two-Wattmeter Three-Phase Power Measurements
A two-wattmeter power measurement can be performed on a Delta or Wye winding (Figure 5). In either case, voltage is measured line-to-line on two phases, with both referenced to a common point. In the examples shown in Figure 5, the measurements are VA-C and VB-C, with C being the common reference point. Current is also measured on these two phases, so we have the A current and B current both flowing into the neutral point C.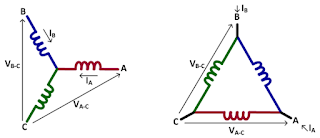 |
| Figure 5: The two-wattmeter method of making three-phase power measurements works on either Delta or Wye windings as shown |
This method works because we can make mathematical assumptions. If we know two of the three voltages and currents, we can solve for the third. According to Thevenin's Theorem, we can take a line-to-line voltage and a line current, and a line current and a line-to-line voltage, and calculate the three-phase power directly from that information. The mathematical assumptions are as follows:
- Σ(IA + IB + IC) = 0
- Σ(VA-B + VB-C + VC-A) = 0
Our final post in this series will tie everything together by reviewing an example of a three-phase power measurement from a 480-V motor drive.
Previous posts in this series:
Back to Basics: The Fundamentals of Power
Back to Basics: Fundamentals of AC Line Power (Part II)
Back to Basics: Three-Phase Sinusoidal Voltages
More Basics of Three-Phase Sinusoidal Voltages
Back to Basics: AC Sinusoidal Line Current
Power Calculations for Pure Sine Waves
Power Calculations for Distorted Sine Waves
No comments:
Post a Comment