Measuring Dead Time in 48 V Power Converters, Part 2: Dynamic Measurements

Figure 1. P1 and P2 measure dt@lvl over the entire acquisition,
while P3 and P4 measure dt@lvl for only a single operational
cycle of zoom traces Z1 and Z3.

A primary engineering task for 48 Volt power conversion systems using bridge topologies is to ensure adequate dead time to prevent catastrophic shoot through occurring when both HI and LO FETs conduct at the same time. Being able to accurately measure dead time is therefore of critical importance. Part 1 of this series dealt with the basic dead time measurement. Part 2 will deal with studying the dynamic changes in the dead time measurement using statistical tools like tracks and histogram functions.

As we learned in part 1, the dead time delay is measured using two instances of the measurement parameter Delta Time at Level (dt@lvl) as shown in Figure 1.

In the Figure 1, the dt@lvl parameters P1 and P2 show the value of the last measurement in the acquisition which contains 10,000 switching transitions. The parameters P2 and P4 measure only the single timing cycle shown in the zoom traces. (Click any image to enlarge it and see the detail.)

The values of both parameters are different, and you should ask the question: how does dt@lvl vary with time? To find the answer, turn on the measurement parameter statistics, as shown in Figure 2.

Fig 2. Parameters measure all instances of the
measurement occurring in the waveform;
statistics summarize all the values collected.

P1 and P2 have each collected 10,000 values of dt@lvl, and the statistical table shows the last value, mean, minimum, maximum, standard deviation and number of values reported. At the same time, the parameters P3 and P4 have only measured one value each because the zoom traces Z1 and Z3 had only a single cycle of the measured voltage signals. P1 ranges from a maximum of 1.675 ns to a minimum of 1.347 ns, while P2 ranges from 1.382 ns to 1.043 ns. The minimum values of both parameters are positive, indicating that shoot though has not occurred.

Using the Track Function

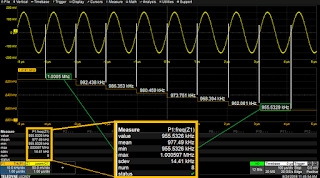Fig 3. A track of frequency parameter P1
plots frequency vs. time over eight cycles.
The track is sampled at the same rate as the
source waveform and remains time synchronous.

The time-based parameters are measured for each cycle in the acquisition. P1 and P2 in the example above store 10,000 instances of that measurement being made on the source waveform. The track function plots those values against time. The track function is time synchronous with the source waveform of the parameter.

Figure 3 shows the track of a frequency measurement taken from another test, for purpose of illustration. Frequency decreases from ~1 MHz to ~956 kHz in eight steps corresponding to the cycles of the source waveform, which are clearly visible on the track.

The tracks of the two dt@lvl parameter measurements are shown in Figure 4.

Fig 4. The tracks of P1 and P2 show random variation
between the min. and max. of each parameter.

The track view confirms graphically that there are no delay values that are negative. Each value in a track matches up with its source on the VgsLo or VgsHi waveform. This allows any anomalous events seen on the track to be matched to the source for analysis.

The maxima of the P1 dt@lvl measurement, 1.674 ns, was located on track F5 (top right grid) by using parameter P3 to apply the Maximum measurement to the track. Tracks can be measured just as can their parameter source waveforms.

The measurement x@Max was also applied to track F5 to determine the horizontal, or time, location of the maximum value. This value was then used to center the zoom traces Z1 and Z3, bringing the two edges with the maximum delay into view in the center of the lower left grid. A cursor was placed at that point in time to mark the location on all the traces. So, from an observable event on the track function, a specific set of edges were located and displayed for further analysis.

Using Histicons and Histograms

Fig 5. Histograms of P1 and P2 display the
distribution of the dt@lvl parameter values.
Histogram parameters read the mean,
std dev and range of each histogram.

Histicons, iconic histograms, below each parameter in the Measure table show the distribution of parameter values. The histogram plots a bar chart of the number of measurements falling within a small range of values called a bin. The scale of the histogram function reflects the total number of measurements (vertical) vs. measured value (horizontal). It is an estimate of the probability of a given value occurring. Double-clicking on the histicon will open a full histogram for analysis, as shown in Figure 5.

The histogram itself provides a visual representation of all the measured parameter values. The bins farthest away from the mean (highest bar) contain the histogram tails, which hold the values with the lowest probability of occurrence. Seeing the delay data in this way makes it easy to determine the error margin for the deadtime.

The shape of a histogram is related to the underlying physical process causing variation. See our earlier posts on histograms listed below for more about histogram shapes. The shape of the histograms of the dt@lvl parameters in F9 and F11 is close to a Gaussian, or Normal, distribution. That implies that the process underlying the variation in values is random. The most probable source is edge jitter.

Histogram measurements can be used to quantify the histogram. The oscilloscope used in these examples has thirteen distinct measurements exclusively for histograms. In Figure 5, histogram measurements are used to determine the mean, standard deviation and range of values represented by each histogram.

Using Statistics to Test Tolerances

Fig 6. The setup for Pass/Fail testing offers
choices based on the statistical mean (µ)
and standard deviations (sigma).

The information from measurement statistics, be it from the parameter or histogram measurements, can be used to set measurement limits for Pass/Fail testing, provided statistics are turned on for the measurement. The setup for a Param(eter) Compare Pass/Fail test includes selections based on the current mean or standard deviation offsets of the source measurement (Figure 6). The advantage to this method is that limits can be set according to tolerances, rather than on absolute values.

Learn more from the on-demand webinar, Best Practices for Debugging 48 V Power Conversion Systems.