 |
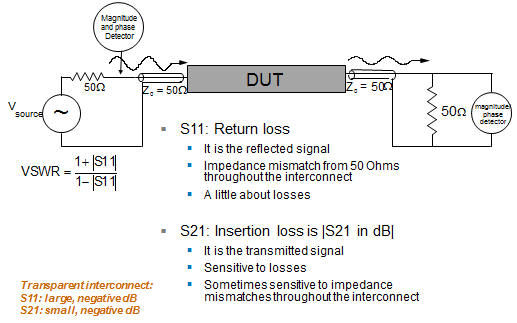
| Figure 1: Measuring S-parameters of a two-port interconnect |
As Figure 1 depicts, the second (or output) port in this DUT would be connected to a second port on our network analyzer, again using a precision 50-Ω cable. The first network-analyzer port, shown at left in Figure 1, provides an input signal from which we can now measure both S11 and S21 for this DUT.
S11 tells us about any impedance variations and lossiness in the DUT. If there's a significant amount of loss, that will show up in a lessened amplitude in the reflected waveform. As shown in Figure 1, VSWR is easily calculated from S11.
With the output port of our interconnect connected to our network analyzer, we can now measure S21. Insertion loss is the magnitude of S21 in decibels and is the transmitted signal coming out of the far end of the interconnect. Primarily, S21 tells us about the amount of loss in the interconnect, but it also tells us something about impedance and reflections. Any energy that is reflected back out of the input port 1 is obviously not going to appear at the output port 2, which speaks to impedance.
 |
| Figure 2: The connection between insertion loss and return loss |
Now that we've discussed both insertion and return loss, let's take a look at the connection between them (Figure 2). Generally, we're interested in the waveform that is transmitted through to port 2 of the interconnect, but it's interesting to see how the reflected waveform affects what is transmitted.
It would seem logical to assume that the incident waveform would be equal to the reflected waveform plus the transmitted waveform, or S11 + S21 = 1. That would hold true if there were conservation of voltage, but there isn't. There is, however, conservation of energy, and the energy in a wave is roughly equal to the square of the voltage. So a better approximation would be 1 = S112 + S212 + any losses in the system. Those losses might be conductor loss, dielectric loss, crosstalk, coupling, or radiation. If we were to assume a lossless interconnect, we would have quite a solid relationship between the reflected and transmitted signals. Insertion loss would be S21 = √1 - S112.
 |
| Figure 3: Insertion loss plotted against return loss in dB |
But how do you measure the amplitude of the incident wave and the reflected wave if they are on the same port? There are a few ways. With a frequency-domain instrument, a directional coupler will pick off the signal in only one direction. With a time-domain instrument, use a fast edge for the incident waveform. The sampler also can discern the reflected waveform because it happens later in time.
An important consideration: What level of reflected signal will significantly impact the transmitted signal? The plot in Figure 3, which uses the equation at center, shows S21 in the vertical axis and S11 in the horizontal axis.
At -20 dB of return loss, the reflection is 10% of the incident waveform's amplitude (see note below). But even with that 10% reflection, there is nearly no impact on insertion loss. At -10 dB, some 30% of the signal energy is being reflected but with only -0.5 dB of impact on insertion loss. So we can have a good amount of reflected energy without noticing much of a difference in transmitted signal.
The bottom line? If you want to ensure that return loss doesn't have much effect on insertion loss, you want to hold return loss to a maximum of -13 dB. What would -13 dB of return loss mean in terms of an impedance discontinuity in our interconnect? If it's a 50-Ω transmission line, we're talking about a 12-Ω impedance variation. So if impedance doesn't vary more than that, you won't see much impact on insertion loss. It's a decent rule of thumb for understanding how much return loss is too much in your interconnect.
Next, we'll start looking at a few common patterns for S11 and S21, where they come from, and what they tell us about an interconnect.
Note: There is a healthy amount of confusion in the industry about how to interpret the dB value of S-parameters, and we may have caused confusion by using the word "energy." S-parameters are a ratio of amplitudes, such that in dB, you follow the formula Sxy_db = -20log (Vout/Vin), where Vout and Vin are the voltages at ports x and y, with other ports terminated (typically at 50 ohms). So at -20 dB, the amplitude is down by a factor of 10: Vout/Vin = 0.1. For an S11 of -10dB, the amplitude of the reflection is down to 31.6% of the input. When determining the energy (or power) that is not reflected, we need to do the appropriate squaring, as mentioned in the article. (S21 = sqrt(1-S11^2). This evaluates to an S21 = 0.949, or ~0.5 dB. For more information, we recommend this informative article by Eric Bogatin.
4 comments:
Hi,
Appreciate the document and its use for fresh engineers to understand S-parameters and its consequences. I just had one doubt, how -10dB corresponds to 30% of the signal energy. I believe -10dB corresponds to 0.1 ratio which means 10% reflection!!
Could you please elaborate,
-Darshan Parmar
& -0.5dB of S21 meaning almost 90% of the wave is transmitted i.e. output left after 10% of loss as reflection...
Darshan, thank you for your comments! We have clarified the post and added some information in a postscript that may help address your comments. Let us know if you have more to add.
Thanks for clarifications!!
Post a Comment