How Equalization Works in 10x Passive Probes

Figure 1: The adjustable equalization circuit on the oscilloscope
end of the coaxial cable compensates for the 10x passive
probe's inherent low-pass filter characteristics

We've been discussing 10x passive probes and their inner workings; our last post covered all the ways in which a 10x passive probe is apt to be a liability. They'd be basically unusable for any measurements at all but for one attribute: their equalization circuit (Figure 1). Without it, the 10x passive probe makes a pretty good low-pass filter, but the equalization circuit counters that with a high-pass filter to balance things out.

Referring again to Figure 1, there's a 9-10 pF bypass capacitor in parallel with the 10-MΩ input impedance at the tip of the probe. High frequencies will pass through the capacitor, and they'll also see the capacitance at the oscilloscope end of the probe cable. The combination of the low-pass response of the series resistor and shunt capacitance to ground and the high-pass response of the compensation capacitor results in a flat, high-bandwidth response overall.

Figure 2: This trimmer capacitor is the
key to flattening the probe's
frequency response

We want the time constants for the high-pass filter and low-pass filter to be matched so that their pole frequencies are the same; that's what gives our 10x passive probe its overall flat frequency response. If there's too much high-pass filtering, we'll have a peak response, and if there's not enough, we'll have a low-frequency response. We're looking for just the right balance.

That's why the adjustable capacitor, which is typically found at the end of the cable near the coaxial connector, enables us to change that capacitance so that the time constant for the capacitor and resistor at the oscilloscope input is the same as that for the 9-MΩ resistance and capacitance at the business end of the probe. Once we match those time constants, we achieve the flat, uniform frequency response we want to see.

Figure 3: Shown are examples of under-compensation,
over-compensation, and proper compensation using the
probe's trimmer capacitor

That little adjustment trimmer at the end of the 10x passive probe's cable (Figure 2) adjusts that equalization circuit. Here's how to get things squared away: Plug your probe into the oscilloscope's CAL output on the front panel. That output gives you a fast-edge, clean square wave. You want to adjust that trimmer capacitor until you see a signal on your oscilloscope's display that looks like the one at center in Figure 3. If it looks like either of the other two traces shown, you've not yet matched the time constants of the two filter circuits. You can find more detail about this trimmer adjustment here.

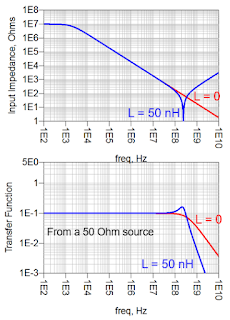Figure 4: Input impedance and transfer
function plots for a 10x passive probe

In terms of performance of the 10x passive probe, at frequencies above about 1 kHz the input impedance is mostly made up of that 9-10 pF capacitance. At low frequencies, we'd see the 9 MΩ of the series resistance plus the 1 MΩ of the oscilloscope's input impedance, but there's that 10-pF capacitance shunting that resistance. Thus, the impedance we see looking into the probe is equivalent to about 10 pF, which means that the impedance will drop off as we go higher in frequency. At DC, it's a 10-MΩ input, but it looks like a capacitive impedance at higher frequency. So it's important to take that into account when using the probe.

Another complication is the potential for loop inductance between the signal and return paths. The amount of inductance depends on how we make the connection, but it will have an impact on bandwidth. The L and C result in a series LRC response as seen at the probe tip, which will show up as an impedance dip at higher frequencies and in the transfer function (Figure 4).

We've built what is essentially a two-pole low-pass filter that has some peaking in its response, which is why, if there's some inductance in the return path, we'll see some peaking in the hundreds of MHz range. If our source impedance of the DUT is 50 Ω, the nominal drop in transfer function will be flat with a -20 dB attenuation with a -3 dB drop from the passband region at a couple hundred MHz.

It's important to bear in mind that the input impedance is capacitive as we go to higher frequencies, which ultimately limits the bandwidth to the hundreds of MHz range. Any additional inductance in the tip will further decrease the bandwidth and potentially introduce ringing. This is why we always want low inductance in the tip.

We'll continue exploring the performance of the 10x passive probe in an upcoming post.

Previous posts in this series:

Putting Probes in Perspective

Secrets of the 10x Passive Probe