Probing Techniques and Tradeoffs (Part III)

Figure 1: Bandwidth is defined as the frequency at which
the ratio of the displayed amplitude to the input amplitude
is -3 dB (or 0.707)

Any discussion of oscilloscopes and/or probes must include the topic of analog bandwidth. Bandwidth is one of a short list of key specifications for a testbench setup. All oscilloscopes and probes come to market with a bandwidth specification, which is defined as:

The frequency at which the ratio of the displayed amplitude to the input amplitude is -3 dB (or 0.707).

This is known as the "-3 dB point," or the half-power point (Figure 1). At this frequency, a sine-wave input signal is attenuated to 70.7% of its true amplitude. Any higher frequencies will likely be distorted on the display, making accurate measurements and calibration impossible.

Figure 2: The Fourier expansion of a square wave reveals its
composition of a fundamental frequency and an infinite
number of harmonics (right). There is a direct relationship
between frequency content and signal rise time (left)

For example, if my oscilloscope is specified with a bandwidth of 3 GHz and I'm measuring a sine wave with frequency of 1 GHz and amplitude of 1 V, the oscilloscope will indicate a signal amplitude of 1 V. However, if I input a 3-GHz, 1-V sine wave, the signal will be attenuated by about 3 dB, and the instrument will show an amplitude of about 700 mV.

The Fourier expansion of a square wave shows why bandwidth is worth caring about. Square waves represent the summation of a fundamental frequency and an infinite number of harmonics. One can see how the shape of a square wave changes with the capture of more harmonic content. It's clear that there is a direct relationship between the frequency content and the signal's rise time  (Figure 2).

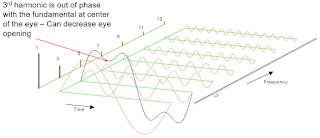Figure 3: Having enough bandwidth is key to gaining
insight into the frequency content of a signal

Figure 3 provides an example of how having enough bandwidth to capture the fundamental plus the third harmonic shapes the signal. Note that in this example, the third harmonic is out of phase with the fundamental at the center of the eye. This illustrates why it's so important to capture enough harmonic content so as to understand the signal's content and how it influences the overall shape.

There is another bandwidth relationship to consider, and that's the relationship between analog bandwidth and the bit rate of the signal. As a general rule, the oscilloscope's analog bandwidth should be about 2.5X the signal's bit rate. If, for example, we're observing a 25-Gbit/s square wave, the frequency content includes a 12.5-GHz fundamental, a 37.5-GHz third harmonic, and a 62.5-GHz fifth harmonic. So in this case, depending on the power spectral density of the signal, there could be significant power present out to the fifth harmonic. Thus, we'd recommend an oscilloscope with a 65-GHz bandwidth.

We'll pick up on the topic of bandwidth in our next installment. Meanwhile, please visit the prior entries in this series of posts:

Probing Techniques and Tradeoffs (Part I)
Probing Techniques and Tradeoffs (Part II)