Applying Multi-Stage, Multi-Rate Digital Filtering

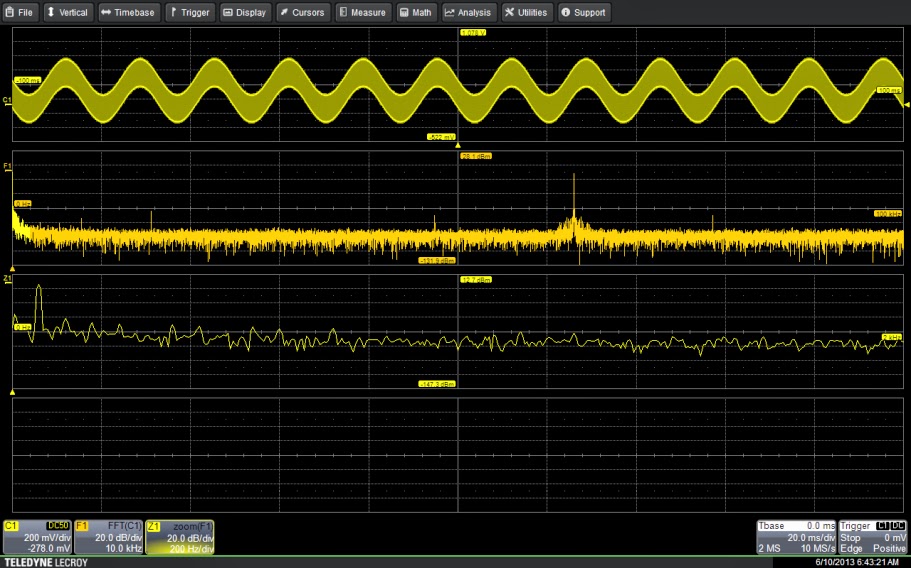
Figure 1: The input signal shows both the desired 63-kHz signal
along with a 60-Hz component. Zoom trace Z1 shows the
60-Hz component in detail.

A while back, we posted some basics on how to apply digital filters to sort out signals with undesirable elements riding on top of them, i.e. a square wave that's being corrupted by a sinusoidal signal creeping in from somewhere in your system design. Now, let's look at how to extend the range of cutoff frequencies for digital filters, allowing them to be used even more effectively.

With Teledyne LeCroy's Digital Filter Package (DFP2), users can select any of seven standard filter types or define a custom filter for application to measured data. You can specify a range of pass-band limits and transition (roll-off) widths for any filter, which are implemented as digital finite impulse response (FIR) filters. The range of band-edge frequencies is a function of the oscilloscope's effective sampling rate. Using the available math traces on Teledyne LeCroy oscilloscopes, you can implement multi-stage, multi-rate filters to extend the range of the DFP2 package's filter limits.

Let's see how this works with an example of a signal (Figure 1). This is a signal you'll commonly find in switching power-supply measurements. The measured waveform contains a 63-kHz pulse-width-modulated signal riding on top of a 60-Hz sine wave. Removal of the 60-Hz signal requires a high-pass filter with a pass-band edge above 60 Hz.

Figure 2: Shown is the series of math operations used
to implement a multi-stage, multi-rate digital filter

While this filter can be implemented with the DFP2 filters, doing so at a 10-Msample/s sampling rate means using filters with a very large number of taps. If we want to reduce the filter size, we must reduce the sampling rate. There are two ways to go about this. One is to reduce the length of the oscilloscope's acquisition memory. The other is to decimate the data using the sparse math function.

Reducing the sampling rate increases the possibility of aliasing the data, especially with a harmonic-rich signal like this one. To limit the possibility of aliasing, the data can be sampled at a high rate and then low-pass filtered, using a digital filter, before decimation. This combination of filtering and decimation before performing another filtering operation on the data is called "multi-stage, multi-rate" digital filtering. It allows you to reduce the effective sampling rate with minimal risk of aliasing, thus extending the usable range of the DFP2 filters.

So here's the multi-stage, multi-rate implementation (Figure 2). The upper trace is the acquired waveform sampled at 10 Msamples/s. The goal is to reduce that sampling rate by 10:1. We accomplished this by first low-pass-filtering the acquired data with a bandwidth of less than 50% of the desired effective sampling rate of 1 Msamples/s.

Figure 3: Shown is a comparison of the input and output
spectra with a 40-dB reduction of the 60-Hz component
in the lower (output) trace. The right side shows the
60-Hz component before and after filtering.

Math trace F2 is the signal after low-pass filtering with a bandwidth of 500 kHz. Math trace F3 applies the sparse math function, which is used to decimate waveform data. The decimation ratio of 10:1 is set using the Sparsing Factor variable in the Math dialog box (accessed using the Math Setup menu). The resulting decimation is 10:1 and the effective sampling rate is 1 Msamples/s.

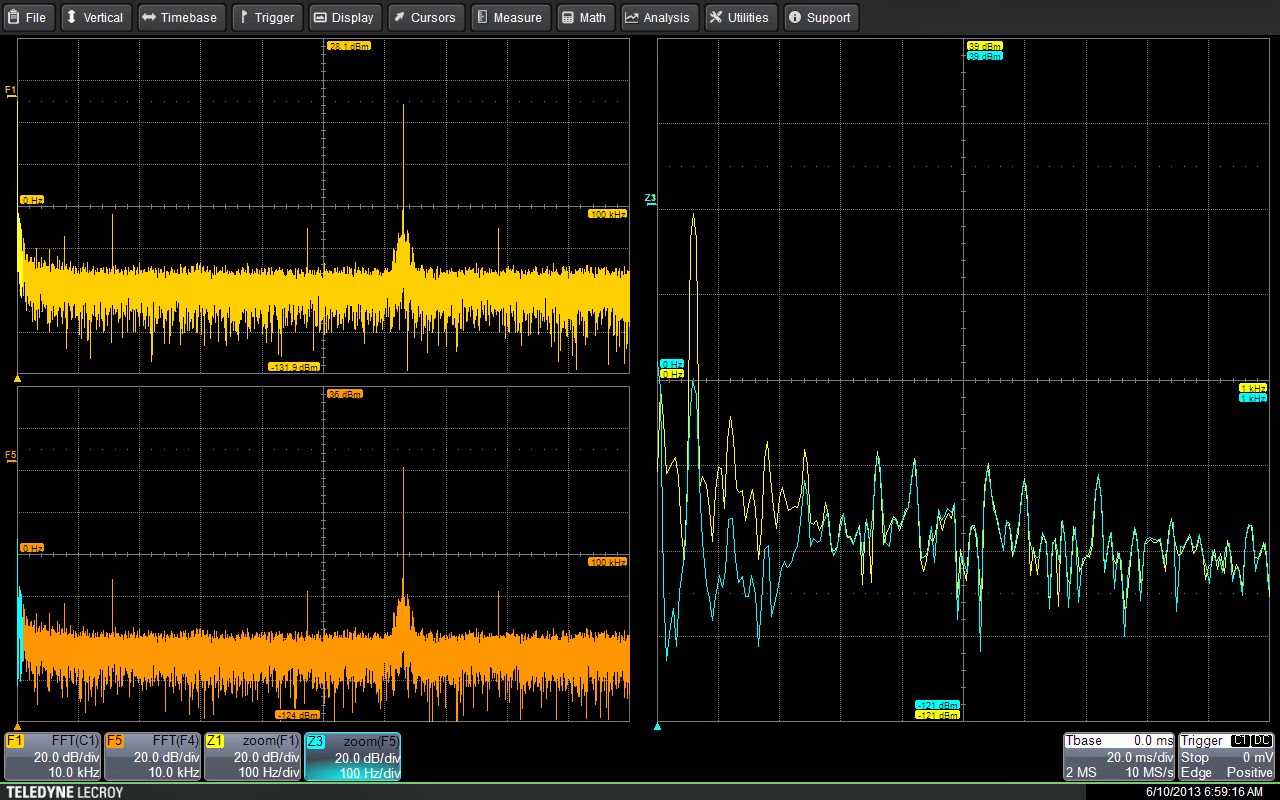
Math trace F4 is the setup for the high-pass filter. The cutoff frequency is 200 Hz with a transition zone width of 50 Hz. Note that the 60-Hz component has been greatly reduced by the filtering process.

In Figure 3, a comparison of the input and output frequency spectra shows that the 60-Hz component has been reduced by 40 dB. This can be seen in the right-hand zoom trace comparison. The high-pass filtering does not affect spectral components above 300 Hz.

With this example, we can see how multi-stage, multi-rate filtering extends the usable range of the DFP2 digital filters.