Back to Basics: What is an FFT?

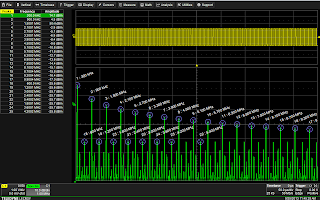
Figure 1: An FFT of a 300-kHz square wave.

In an earlier post, we discussed the basics of setting up a fast-Fourier transform (FFT) on an oscilloscope, and why you'd want to use an FFT to get a frequency-domain view of a time-domain signal in the first place. It might be a good idea to take a step back and dig into just what an FFT is (Figure 1).

The theory behind FFTs makes an assumption, which is that the time-domain signal being transformed into a frequency-domain spectrum is of infinite duration. Obviously this is not achievable, so the compromise between theory and practice is to view the time-domain signal as consisting of an infinite series of replicas of itself.

In using FFT on a time-domain signal, what's really happening is that the signal is being separated out into its constituent frequency components, essentially diluting its spectral energy in some number of frequency bins corresponding to multiples of the frequency resolution Δf. The capture time, T, determines the frequency resolution of the FFT (Δf = 1/T). Meanwhile, the sampling period and record length set the maximum frequency span that can be obtained (fNyq = Δf*N/2).

All of the above could, of course, be worked out mathematically as a discrete Fourier transform. But to do so even on an eight-sample signal would involve 64 complex multiplications. A signal with 1024 samples balloons out to over 1 million multiplications.

Thus, an FFT operation on an N-point time-domain signal is comparable to passing the signal through a comb filter consisting of a bank of N/2 filters. All of these filters have the same shape and width and are centered at N/2 discrete frequencies, meaning that there are N/2 frequency "bins." The distance in hertz between the centering frequency of any two neighboring bins is always Δf.

Table 1: FFT window types and their characteristics.

The way your FFT turns out is dictated to a large extent by the "window" chosen for the operation (Table 1). The window type defines the bandwidth and shape of the bank of filters applied to the time-domain signal. The weighting functions imposed by these windows control not only the filter response shape, but also noise bandwidth and side-lobe levels. Ideally, the main lobe should be as narrow and flat as possible to effectively discriminate all spectral components; meanwhile, all side lobes should be infinitely attenuated.

You can think of choosing a window type along the lines of choosing a camera lens for a given photo. Some experimentation might be in order. As shown by the table, some windows will lend themselves better to certain signal types than others, with tradeoffs between leakage and frequency resolution.