About Windowing in Fast Fourier Transforms

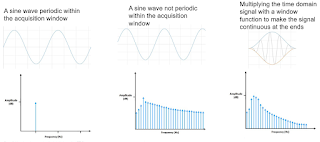
Figure 1: Windowing a waveform that's not periodic within
the acquisition window reduces spectral leakage

The second artifact in FFT calculations is more serious and is also the source of some confusion. A good source for information on this topic of windowing is an application note published by National Instruments.

Consider an acquisition window (top left in Figure 1) in which we're looking at a frequency component that's a multiple of 1/acquisition window. This means we have an exact integral number of cycles in that window. Not only that, but whatever voltage it had at the beginning of the window is the same voltage it has at the end of the window. This is a truly repetitive signal. In such an (ideal) situation, the spectral information is very pure with no leakage. We can get individual sine wave components when we perform the FFT.

Now, what if we have that same frequency component but the acquisition window is slightly off, with the signal shifted so that we're not beginning and ending at the same voltage (top center in Figure 1). In keeping with the assumption critical to FFTs that the signal is repetitive, we append window's worth of data to window's worth of data, and when we do so, we create a discontinuity between where the voltage is at the end of one window's worth of data to where it is at the start of the next window's worth of data.

As a result of that discontinuity, we add artificial high-frequency components that pollute the other spectral content, even though we still have one pure sine wave. At bottom center of Figure 1 we see what that spectral content looks like.

The remedy for this leakage of spectral information at one frequency into the higher-order frequencies is to slightly distort the waveform and add a windowing function to it (top right in Figure 1). The distortion engineers the starting voltage in the acquisition window so that it matches the ending voltage. In doing so, we introduce an artifact compared with a pure sine wave, but we also dramatically reduce the leakage of information from that pure sine wave to the higher-order frequencies (bottom right in Figure 1).

That's a brief explanation of why you might employ windowing in performing a fast Fourier transform. In the next installment, we'll look at different windowing functions and which are best to use in most circumstances.

Previous posts in this series:
Getting From the Time Domain to the Frequency Domain
About Data Truncation in Fast Fourier Transforms