About Data Truncation in Fast Fourier Transforms

Figure 1: The first precondition of using the Fourier transform
is a repetitive signal

Our last post discussed how time-domain signals acquired by an oscilloscope might be translated into the frequency domain using the discrete Fourier transform. We noted that using the Fourier transform only works if our signal is repetitive (Figure 1), and that it allows us to identify only harmonics of the first harmonic frequency, which is 1/acquisition window. Moreover, the discrete Fourier transform, if used on a large number of data points, is relatively slow to calculate.

Enter a little mathematical trick known as the fast Fourier transform (FFT). The FFT will only work if we have a number of data points in our acquisition window that corresponds to 2ⁿ points. That's to say that there has to be, say, 256 points, or 512, 1024, or 4096. Then, we can employ some matrix math methods to dramatically reduce the calculation time for the frequency components. Additionally, the discrete Fourier transform's requirement that the waveform be repetitive still holds for the FFT.

Figure 2: An example of an FFT screen capture

We'd said previously that the lowest frequency in the spectrum, the first harmonic, is equal to 1/acquisition window. The highest frequency is related to the sample rate (Nyquist theorem). If we're sampling at, say, 10 GS/s, the highest frequency component we can resolve is half of that, or 5 GHz. It's also important to note that the front-end amplifier bandwidth of the oscilloscope being used limits the highest usable frequency we can see in the waveform.

Figure 2 depicts an example of an FFT screen capture. The acquisition window spans 10 ms, and thus the resolution is 1/0.01s or 100 Hz. The sample rate is 250 MS/s, making the maximum frequency component 0.5 x 250 MS/s or 125 MHz.

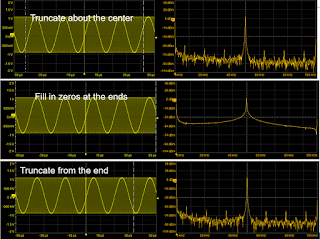Figure 3: The best measurement practice is to select
the option to "truncate about the center"

There are two artifacts to watch out for when performing FFTs. First, we have to use 2ⁿ data points. Thus, if our acquisition window comprises a very large number of data points, we can't use all of them in the FFT. This means that the data must be truncated. Teledyne LeCroy's oscilloscopes offer three truncation options: truncate about the center, fill in zeroes at the ends, and truncate from the end (Figure 3). The best measurement practice is to truncate about the center. That's where the trigger point usually is, and it's also where the most useful information tends to be.

What that means is that we'll use data about the center of the acquisition window that's in the form of 2ⁿ data points. Whatever data is left over is discarded for purposes of the FFT. If we have, say, 2 million data points in the acquisition window, the highest value we can use in the FFT is 2²⁰ data points, which works out to 1,048,576 points.

The second artifact in FFT calculations is more serious and is also the source of some confusion. We'll cover FFT windowing in our next post.

Previous posts in this series:
Getting From the Time Domain to the Frequency Domain