Back to Basics: Three-Phase Sinusoidal Voltages

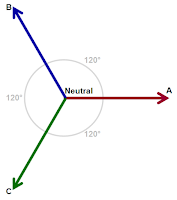
Figure 1: Three-phase AC voltages
consist of three voltage vectors

In a previous post, we briefly covered the basics of single- and three-phase AC power systems. Single-phase systems, as we've noted, comprise a single voltage vector with a magnitude (in VAC) and a phase angle. Of course, a three-phase voltage consists of three voltage vectors and three phase angles. This installment will go on to describe three-phase AC voltages in similarly brief fashion.

As mentioned above, three-phase AC sinusoidal voltages consist of three voltage vectors (Figure 1). By definition, these vectors are "balanced," being separated by 120° in phase, and being of equal magnitude. Moreover, the sum of all three voltages is equal to zero volts at the central neutral point.

Typically, the three phases are designated A, B, and C. However, you may see other conventions used for these designations, such as 1, 2, and 3; L1, L2, and L3; and R, S, and T.

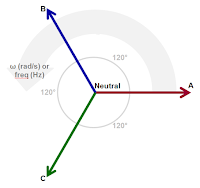Figure 2: Vectors rotate at a given
frequency with constant phase separation

Like single-phase voltages, three-phase AC voltage vectors rotate at a given frequency, which typically is 50 or 60 Hz for utility-supplied voltages. As they rotate together, the vectors maintain their 120° phase separation (Figure 2). The voltage is generated by the utility using a rotating machine, i.e., a "generator." The generator uses a rotating magnetic field to induce a voltage in its stator. And again, like single-phase voltages, the resulting voltage vectors have magnitude and phase values.

The resulting time-varying, "rotating" voltage vectors appear as three sinusoidal waveforms. They are separated by 120° in phase and are of equal peak amplitude.

The voltage value is calculated as: V_x * sin(α), where V_x is the magnitude of the phase voltage vector and α is the angle of rotation (in radians).

There are a variety of reasons for using three-phase AC voltage:

• It's more efficient to generate power with three-phase generators
• It's easier to manufacture high-power transformers and motors
• Superior control capabilities for low-power motors

Figure 3: There are two ways to
measure three-phase voltages:
line-to-line and line-to-neutral

In three-phase systems, voltage can be thought of, and measured, in two ways (Figure 3). One way is to measure line-to-line, or phase-to-phase. Such measurements may be referenced from V_A to V_B (or V_A-B for simplicity), for example. The second possibility is to measure line-to-neutral; for example, from neutral to V_A (or V_A-N for simplicity). For such measurements, of course, neutral must be both present and accessible.

Note that the line-to-line vectors are longer than the line-to-neutral vectors. Thus, magnitudes of line-to-line voltages are typically larger than line-to-neutral voltages. It's more common to probe and acquire line-to-line voltages, because while a neutral point may not always be present, there will always be the three lines. Also, line-to-line measurements may be converted to line-to-neutral values and vice versa. The differences between them boil down to a 30° difference in phase and a magnitude difference of √3.

Next time, we'll look at the ways in which three-phase connections can be made as well as more details of line-to-line and line-to-neutral measurements.