 |
| Figure 1: AC line voltage is a single-phase vector that rotates at a given frequency |
We refer to AC sinusoidal line voltage by various names: Grid voltage, household voltage, power line, utility power, mains, and so on. They're all the same thing. Most often, the term we hear is "VAC" or just V. What that really means is an RMS (root mean square) voltage rating. You'll hear these terms used interchangeably in the context of discussions of AC line power.
Single-phase AC systems can comprise either two or three wires. Here in the United States, the typical 115-V system carries two wires, while a 240-V system comprises two hot wires and a neutral line.
Three-phase wiring can be of either three or four wires. Multi-phase systems can be of more than three phases; this isn't something that utilities typically provide but it could be achieved locally with some form of power conversion. Most often, four to six phases come into play for redundancy's sake in military/aerospace applications so that even if a phase (or two) fail, the system will remain operational.
When engineers measure AC sinusoidal voltage, it's important to establish a reference point. In a single- or two-phase system, the measurement is typically taken against a neutral line. However, in a three-wire system, the measurement can be from hot line to hot line, or from phase to phase. If it's a three-phase system, measurements can be from line to neutral or from line to line. Remember that a neutral line isn't the same thing as a ground, which is a safety connection from chassis to earth ground. Also, note that the shape of an AC sinusoidal voltage is nominally a sine wave, but it's never a pure sine wave. In the real world, utility voltages always carry some amount of distortion.
How should we think of AC line voltage? Fundamentally speaking, it's a single voltage vector with a magnitude (expressed in volts) and a phase angle. Thinking of it in this way helps one to understand why the voltage attains its sinusoidal shape over time. Typically, a single-phase voltage is referred to as "line voltage."
That single-phase voltage vector, depicted in Figure 1, rotates at a given frequency, which, for typical utility voltages, is 50 to 60 Hz (sometimes that's expressed in radians/s). At any given moment in time, the voltage magnitude is:
V * sin (α)
where V = the magnitude of the voltage vector and α = the angle of rotation, in radians. As the vector rotates, the magnitude changes. Thus, at any given moment in time, the magnitude is as shown above. The resulting time-varying "rotating" voltage vector appears as a sinusoidal waveform with a fixed
frequency of 50 Hz in Europe (period of 20 ms), 60 Hz in the United States (period of 16.67 ms), and either 50 or 60 Hz in Asia. You might see other frequencies associated with power from sources other than utilities, such as 400 Hz in U.S. Navy applications or 25 Hz in mining scenarios.
When you hear someone say "120 VAC," that's an RMS value. Referring to Figure 2, note that the waveform exhibits peak and peak-to-peak voltages that are much higher than 120 V. Peak voltage (VPEAK) is:
√2 × VAC
or, in this case, about 169.7 V. Meanwhile, peak-to-peak voltage (VPEAK-PEAK) may be calculated as:
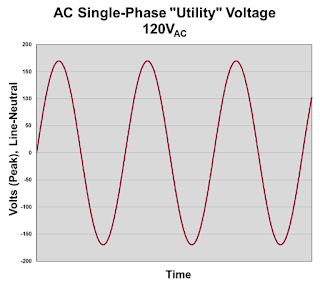 |
| Figure 2: An example of a 120-VAC waveform |
When you hear someone say "120 VAC," that's an RMS value. Referring to Figure 2, note that the waveform exhibits peak and peak-to-peak voltages that are much higher than 120 V. Peak voltage (VPEAK) is:
√2 × VAC
or, in this case, about 169.7 V. Meanwhile, peak-to-peak voltage (VPEAK-PEAK) may be calculated as:
which, in the present case, is 339.4 V. If this AC voltage were to be rectified and filtered, it would be:
VDC = √2 × VAC = VPEAK or, once again, about 169.7 VDC.
While we're on the subject of RMS values, you'll sometimes see references to "true RMS" voltages. "True RMS" is in fact not an engineering-based definition, but rather something that some marketing departments use to describe a mathematically correct RMS calculation as compared to a measurement shortcut taken by inexpensive instruments.
For example, a budget multimeter might calculate RMS using VPEAK-PEAK / √2. The result of such a calculation should actually be referred to as "false RMS," as it is only a valid calculation for a pure sine wave, which can rarely be assumed to be present.
Any sampling technology, such as you find in digital oscilloscopes or power analyzers, will calculate VRMS or IRMS correctly. However, you won't find the makers of these instruments marketing their VRMS calculation as "true RMS."
Next time, we'll examine the basics of three-phase AC sinusoidal voltages.
1 comment:
Immensely exquisite m8
Post a Comment