Oscilloscope Basics: Setting Up FFTs

Figure 1: Capture time determines the
frequency resolution, Δf.

For most of their history, oscilloscopes have been thought of chiefly as a time-domain instrument. That is, an oscilloscope facilitates the observation of changes in a signal's amplitude over time. However, many modern digital and mixed-signal oscilloscopes provide spectral analysis capabilities based on fast Fourier transforms (FFTs) that convert a time-domain waveform into the frequency domain. There are lots of good reasons for taking advantage of this capability. Perhaps the most important is to gain insight into characteristics of the signal that simply are not apparent from a time-domain perspective.

Why would one want to apply FFTs to a waveform? Again, for many signals, there's a lot of information to be had by looking at a spectral representation as opposed to a time-domain view. Take, for example, the frequency response of an amplifier, or oscillator phase noise, and signals encountered in mechanical vibration analysis, among many others; all of these are best observed in the frequency domain.

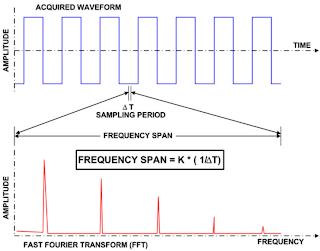Figure 2: The span of the FFT is related to
the sampling rate, 1/ΔT.

If sampling occurs at a rate fast enough to closely approximate the original waveform (usually five times the highest frequency component in the signal), the discrete data that results will uniquely describe the analog input signal. This matters most when dealing with transient signals, because unlike FFTs, a conventional swept-spectrum analyzer will not do the job.

How does one go about setting up an FFT for an acquired waveform? First, consider that the FFT span is related to the sampling rate, and that the resolution bandwidth, Δf, is inversely proportional to the record length. These basic relationships are shown in Figures 1 and 2.

Logically, the place to start in setting up an FFT is with the frequency resolution, Δf. It determines the spacing of samples in the frequency-domain display and is similar to the resolution bandwidth setting in an RF spectrum analyzer.

The Δf is set by the time duration of the time-domain signal that is the input to the FFT. If an acquisition channel is the source, the waveform duration is the capture time, which is ten times the time/division setting of the oscilloscope. The relationship between capture time and Δf is shown in Figure 2.

The frequency span of the FFT is called the Nyquist frequency and is one half of the effective sampling frequency of the time-domain waveform. Teledyne LeCroy oscilloscopes will generally default to the highest sampling rate and therefore the longest span.

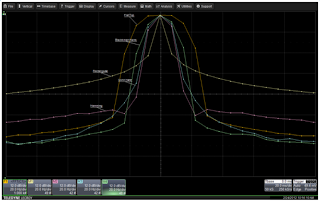Figure 3: The spectral "shapes" of each
of the window weighting functions.

Many oscilloscopes with FFT offer a selection of weighting window functions. You might think of the FFT as synthesizing a bank of parallel bandpass filters; the weighting function then controls the shape of the filter frequency response. They effectively multiply the resolution bandwidth by a fixed factor, called the effective noise bandwidth (ENBW). Weighting functions help reduce the effects caused by performing FFTs on records of finite length. They control sidelobe amplitudes and minimize what's known as "scalloping" or the "picket-fence" effect.

Some oscilloscopes offer the ability to choose the operative FFT algorithm. In the case of Teledyne LeCroy instruments, users may choose between a power-of-two algorithm and a least-primes algorithm. The former runs faster than the latter, but delivers a record length that is not the same as that of the acquired signal. The least-primes algorithm computes FFTs on transform sizes that have lengths expressible as factors of 2^N* 5K. This is highly compatible with the record lengths one encounters in an oscilloscope, which are often multiples of 1, 2, 4, 5, or 10.

Hopefully, the foregoing will help you get started on frequency-domain analysis of your time-domain signals. Let us know if you have questions or issues we can help with!