 |
| Figure 1: Teledyne LeCroy's PP108, a representative passive probe |
A glance at the probe's datasheet will show you its input resistance and capacitance. For a probe with a 500-MHz bandwidth, typical values are C = 9.5 pF and R = 10 Mohms. But one spec that's missing from the datasheet is ground lead inductance; that's because there are numerous ways in which people choose to ground their oscilloscope's probes.
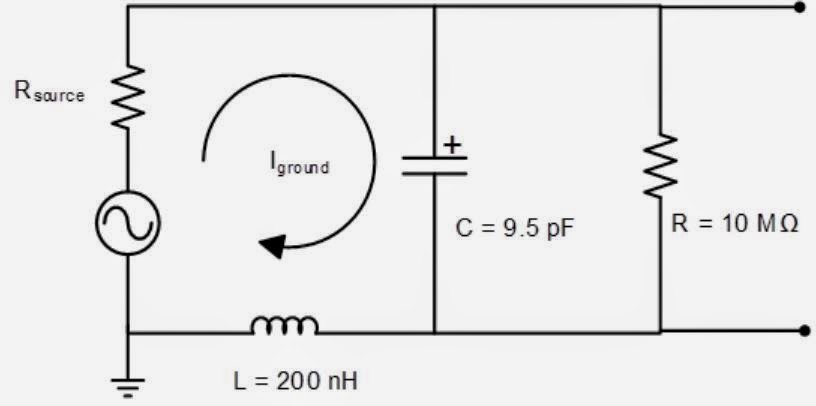 |
| Figure 2: Equivalent circuit model for a passive probe grounded using a long ground lead |
The input resistance of 10 Mohms is large enough to be ignored in most cases. What we want to look at is Iground and the effect that different inductance values will have on the response of this circuit. The voltage across the capacitor is the value measured by the oscilloscope; the voltage represented by the AC source is the signal under test. To get an idea of how these two values will differ, let's look at the transfer function of this series RLC circuit, or the ratio of the voltage across the capacitor, Vc, to the voltage source, Vs. We obtain the transfer function by dividing the impedance of the capacitor by the sum of all of the impedances.
We obtain the transfer function:
 |
| Figure 3: Using copper foil to help minimize the length and inductance of ground connections |
In most cases, though, the ground connection people use is the long alligator-clip lead. What effect does this have on the bandwidth and frequency response of the probe? Well, for starters, if we use this lead, the ground loop of Figure 2 will be at least 10 inches long. If we take 20 nH/inch as a rule of thumb, we can calculate the inductance at about 200 nH. Using a Teledyne LeCroy ArbStudio function generator with a source impedance of 50 ohms, plugging these two values into the transfer function yields this plot:
We can see that the added inductance has moved the -3dB bandwidth of the probe from over 500 MHz to about 175 MHz. Not only that, but the probe's resonant frequency was pushed well within its bandwidth to about 115 MHz. At 65 MHz we can still see an error of 40%. In fact, to keep the error under 10%, we need to limit the frequency to 35 MHz.
In a future post on this topic, we'll look at a practical example to see how this model holds up in the real world.
In a future post on this topic, we'll look at a practical example to see how this model holds up in the real world.


No comments:
Post a Comment